跳到主要内容

提升大语言模型RAG应用的检索效率：向量数据库索引优化策略

· 阅读需 17 分钟

1. 概述​

在一般应用系统开发中，数据存储在关系数据库表中。这种方法很简单，但是随着数据量的增加，管理和检索信息变得越来越困难和缓慢。关系数据库中的一项重要技术是索引，这与图书馆中书籍的存储方式非常相似。无需浏览整个图书馆，而是通过查找书籍索引目录，就可以找到所需的书籍。数据库中的索引以类似的方式工作，加快了查找所需数据的过程。

在基于大语言模型的 RAG 应用中有效地检索知识是提供准确和及时响应的关键。向量数据库的索引策略在加强 RAG 系统性能方面起着至关重要的作用。本文介绍如何使用向量数据库的索引策略来提高 RAG 系统性能。

2. 向量嵌入​

向量嵌入是将文本、图像和音频等对象表示为连续向量空间中的点的一种方法，其中这些点在空间中的位置对于机器学习 (ML) 算法具有语义意义。

3. 向量数据库​

用于存储这些嵌入向量的专用数据库称为向量数据库。数据点以称为“向量”的数组形式存储，

向量数据库是存储和管理向量嵌入的数据库，向量嵌入是高维空间中数据的数学表示形式。在此空间中，每个维度对应于数据的一个特征，数万个维度可用于表示复杂的数据。向量在此空间中的位置表示其特征。字词、短语或整个文档、图像、音频和其他类型的数据都可以向量化。

4. 向量相似性搜索​

在向量数据库中，为了从一组嵌入中搜索和检索数据，我们需要定义一种比较两个向量的方法。这通常被称为相似性度量或相似性指标。我们使用相似性搜索指标（如欧几里得距离（Euclidean Distance）和余弦相似度（Cosine Similarity）等）来计算多维空间中向量之间的相似性，并获取与我们的查询向量最相似的向量。

4.1 欧几里得距离（Euclidean Distance）​

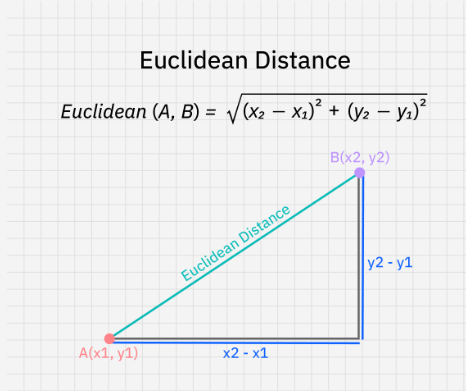
欧几里得距离（Euclidean Distance）是测量两个向量之间的距离的常用方法。是指两点之间直线距离的度量。计算公式为两点对应坐标平方差之和的平方根。通过添加更多项来考虑其他维度，可将此公式扩展到更高维度空间。

Euclidean Distance

4.2 余弦相似度（Cosine Similarity）​

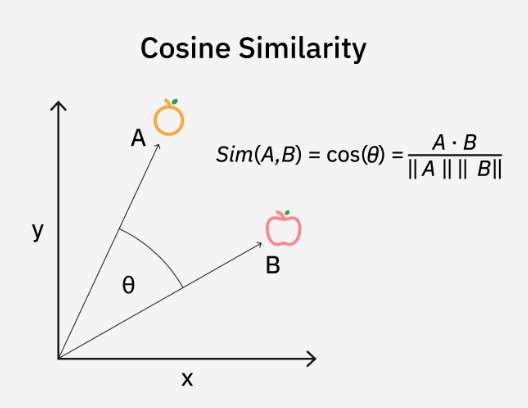
余弦相似度（Cosine Similarity）是一种用于度量两个向量之间的相似度的度量方法。它是多维空间中两个向量之间的夹角余弦值。余弦相似度在计算两个向量之间的相似度时，会考虑向量的方向。

在数学上讲，两个向量之间的余弦相似度 cos(θ) 是以两个向量的点积除以它们大小之积计算出来。

余弦相似度的范围是 -1 到 1，其中：

  • 1 表示向量完全对齐（指向同一方向）。
  • 0 表示两个向量正交（相互垂直）。
  • -1 表示两个向量方向相反。

余弦相似性在处理向量时特别有用，因为它关注向量之间的方向关系，而非大小。

Cosine Similarity

4.3 近似最近邻 (ANN,Approximate Nearest Neighbor)​

虽然前面提到的距离指标可用于衡量向量相似度，但在查询时将所有可能的向量与查询向量进行比较会变得低效且缓慢。为了解决这个问题，我们可以使用近似最近邻 (ANN) 搜索。

ANN 算法并非寻找完全匹配项，而是通过某些距离指标（如欧几里得距离或余弦相似度）有效地搜索与给定查询近似最接近的向量。通过允许某种程度的近似，这些算法可以显著降低最近邻搜索的计算成本，而无需计算整个向量数据库的所有向量的嵌入相似度。

5. 什么是向量索引​

向量索引是一种专门为‌高维向量数据‌设计的索引结构，用于‌在向量数据库中高效地执行近似最近邻搜索‌。

6. 索引策略​

6.1 原始向量索引（Flat Index）​

是一种最基础的索引策略，也可以看做是一种蛮力搜索（Brute Force Search） 。按原样存储所有向量，不做任何修改。并在查询时计算每个向量与查询向量之间的相似度。它简单易行，准确率也很高。缺点是速度慢，不适合处理大规模数据集。

当我们追求极致的准确度，且不考虑速度时，它是正确的选择。如果我们搜索的数据集较小，搜索速度也可以接受，它可能是一个不错的选择。

6.2 局部敏感哈希索引（LSH，Locality Sensitive Hashing）​

通过哈希函数将相似数据映射到同一桶（buckets）中，从而快速缩小搜索范围。 原始数据空间中相邻的点，经过哈希映射后仍保持较高概率位于同一桶内，不相似点则分散到不同桶。这种特性使其能通过哈希表快速定位相似数据，避免全量比对。

6.3 倒排文件索引（IVF，Inverted File）​

它使用 K-means 聚类等技术将整个数据分成几个集群。数据库的每个向量都分配给特定的集群。这种结构化的向量排列允许用户更快地进行搜索查询。当有新查询出现时，系统不会遍历整个数据集。相反，它会识别最近或最相似的集群，并在这些集群中搜索特定文档。

因此，仅在相关集群内而不是在整个数据库中应用蛮力搜索，不仅可以提高搜索速度，还可以显着减少查询时间。

‌6.4 分层可导航小世界（HNSW，Hierarchical Navigable Small Worlds）​

分层可导航小世界 (HNSW) 是构建向量索引最流行的算法之一。它非常快速高效。由于 HNSW 的实现过程略复杂，这里不深入探讨其全部细节，仅重点介绍一些要点。

HNSW 是一种用于索引数据的多层图方法。在最底层，索引中的每个向量都会被捕获。随着图的层级上升，数据点会根据相似性进行分组，从而以指数级的方式减少每层的数据点数量。在单层中，数据点会根据其相似性进行连接。每层中的数据点也与下一层中的数据点相连。如下图所示。

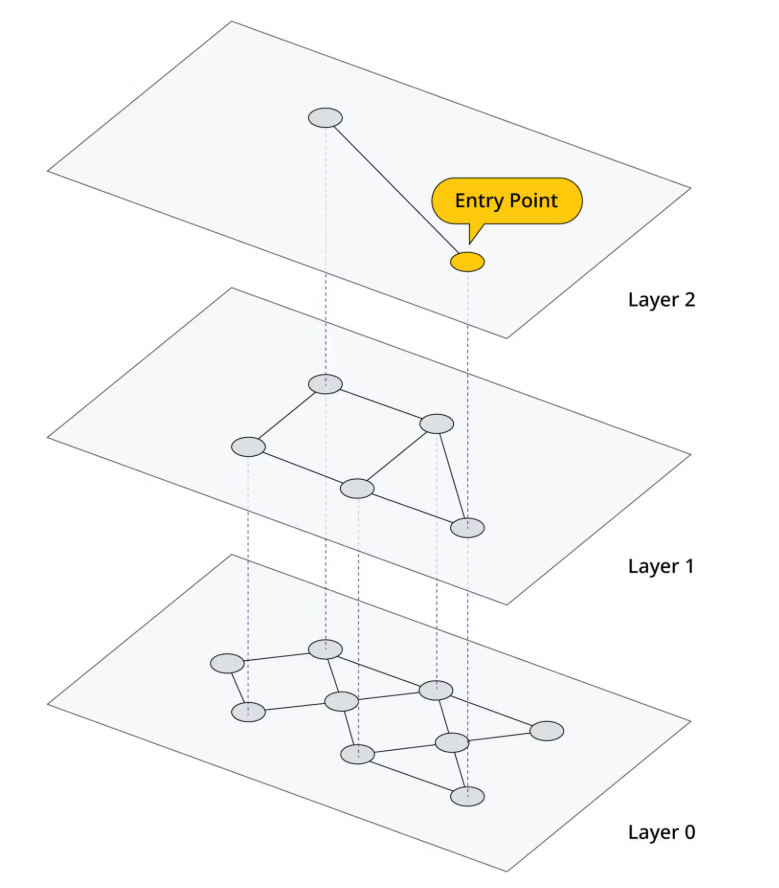
HNSW-1

为了搜索索引，我们首先搜索图的最高层。然后，将图中最接近的匹配项带入下一层，在那里我们再次找到与查询向量最接近的匹配项。我们重复此过程，直到到达图的最底层。

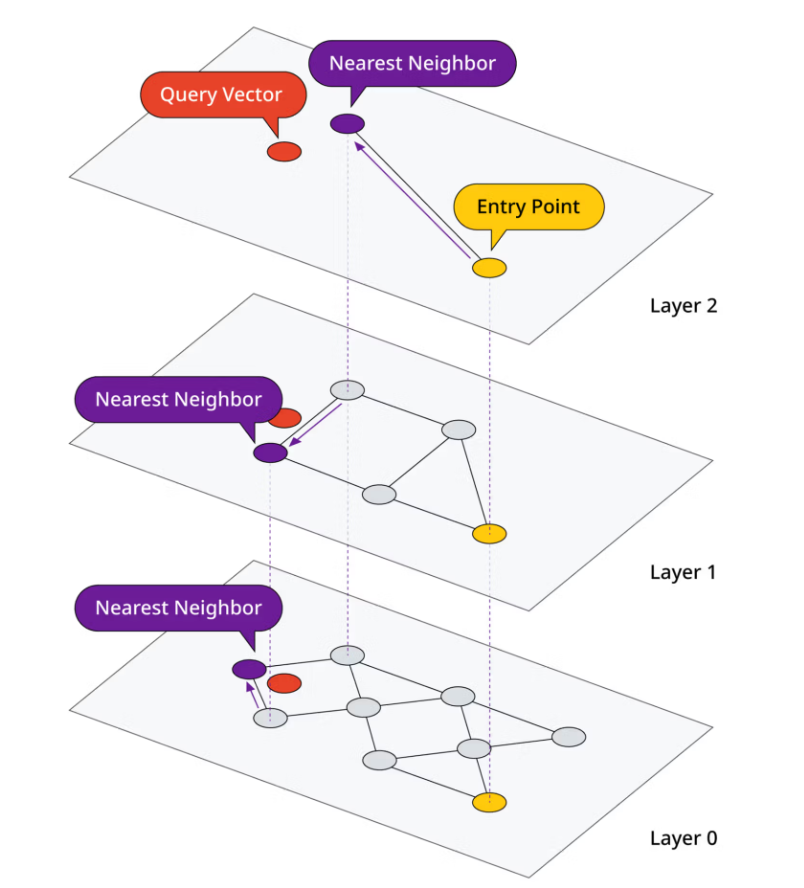
见下图搜索示例。我们从黄色入口点开始，在第 2 层找到与查询向量最近的邻居。然后，我们继续向下逐层查找，在每一层找到最近的邻居。

HNSW-2

6.5 乘积量化‌ Product Quantization (PQ)​

通过划分子空间和量化来压缩向量，是一种高效的向量压缩和相似性搜索技术，主要用于高维空间的向量量化，以便在保持相对高检索精度的同时，大幅减少数据存储和搜索时间。PQ特别适用于那些需要高效进行最近邻搜索的应用场景，如大规模图像或视频检索、推荐系统等。

PQ 的核心思想是将高维空间划分成多个低维子空间，然后在每个子空间内进行独立的量化。具体来说，它将一个高维向量分割成多个较小的子向量，并对每个子向量分别进行量化处理。量化过程中，每个子向量会被映射到一个由有限数量的中心点组成的集合中，这个映射过程通过最小化量化误差来实现。最终，原始的高维向量可以通过这些子向量的量化结果（即每个子向量对应的中心点索引）来近似表示，从而实现了向量的压缩。

6.6 基于树的索引‌ ‌Tree-Based (KD-Tree, Ball Tree)​

KD-Tree：KD-Tree 是一种适用于 k 维空间数据的树形索引结构。它通过递归地将 k 维空间划分为两个子空间来构建树形结构，每个节点代表一个子空间。在检索时，从根节点开始，根据查询向量的值选择进入左子树还是右子树，直到找到最接近的节点。

Ball Tree：Ball Tree是另一种基于树的索引结构，它使用超球体（balls）来划分空间。与 KD-Tree 相比，Ball Tree 在处理高维数据和某些非均匀分布的数据时可能具有更好的性能。

7. 挑战与局限性​

选择合适的向量索引策略需要考虑很多因素。首先，我们要考虑用例。需要多快获得结果？需要结果有多准确？所有向量索引方法都在检索数据和查找相似向量的速度与结果的准确度之间寻求某种平衡。

索引中遇到的另一个挑战是内存占用。不同的算法可能会大大增加运行搜索所需存储的数据量。

在开始执行查询之前，还必须先构建索引。需要考虑构建索引的复杂程度。此外，添加新向量时更新索引的难度如何？如果每次添加新向量时都必须重新计算整个索引，那么我们需要思考索引的更新频率。

8. 需要考虑的因素和如何做出决策​

为检索增强生成（RAG）应用选择向量数据库索引策略时，需要考虑以下因素：

  • 对于小数据集（小于10万个向量），要达到最高准确性：使用原始向量索引（Flat Index）可实现完美召回率，但随着数据集的增长，成本会变得过高。
  • 对于拥有数百万向量的生产系统：HNSW 在搜索速度和准确性之间实现了最佳平衡，使其成为大规模应用的行业标准。虽然它比其他方法需要更多内存，但它的搜索复杂度即使在数据集规模扩大时也能保持稳定的性能。
  • 对于内存受限的环境：IVF+PQ（基于乘积量化的倒排文件索引）可大幅降低内存需求，与原始向量相比，内存需求通常可减少10到20倍，同时只需要在准确性上做出适度妥协。这种组合在边缘部署或嵌入数十亿文档时尤其有价值。
  • 对于频繁更新的集合：局部敏感哈希（LSH）无需重建整个索引即可进行高效更新，这使其适用于文档不断添加或删除的流数据应用场景。

大多数现代向量数据库默认使用 HNSW 是有充分理由的，但了解这些权衡取舍后，必要时你就能针对特定的限制条件进行优化。

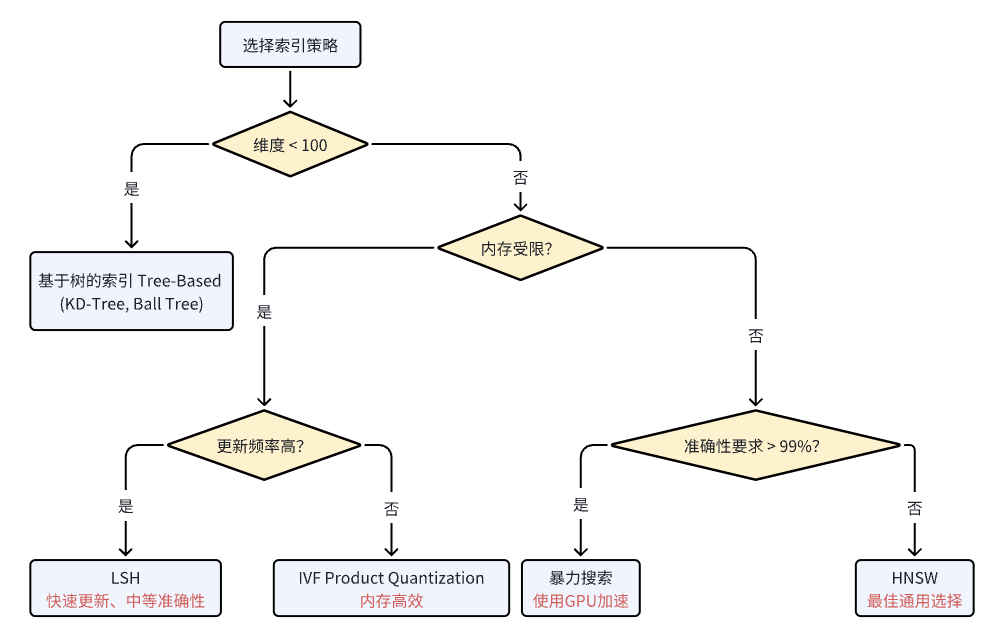
下图展示了一个决策树，用于根据一些限制选择合适的索引策略。可帮助我们梳理关键决策点：

  1. 首先评估数据集大小：对于小数据集（10万个向量以下），原始向量索引搜索仍然可行，并且能提供完美的准确率。
  2. 考虑内存限制：如果内存有限，选择左侧分支，采用如乘积量化（PQ）等压缩技术。
  3. 评估更新频率：如果您的应用程序需要频繁的索引更新，优先考虑像局部敏感哈希（LSH）这样支持高效更新的方法。
  4. 评估搜索速度要求：对于要求超低延迟的应用程序，HNSW一旦构建完成，通常能提供最快的搜索时间。
  5. 平衡与准确性需求：在流程图中向下推进时，根据应用程序对近似结果的容忍度，考虑准确性与效率之间的权衡。

vector-indexing-strategies

9. 结论​

在了解了上述的一些概念和原理后，可以帮助你在必要时做出合适的决策。

对于大多数生产级的检索增强生成（RAG）应用程序，你最终可能会使用 HNSW，或者采用像 IVF + HNSW 这样的组合方法，即先对向量进行聚类（IVF），然后在每个聚类中构建高效的图结构（HNSW）。这种组合在各种场景下通常都能提供出色的性能。